堆排序 heap sort

概述

1. 利用堆(heap)设计的一种选择排序
2. 最坏，最好，平均复杂度为O(nlogn).不稳定排序
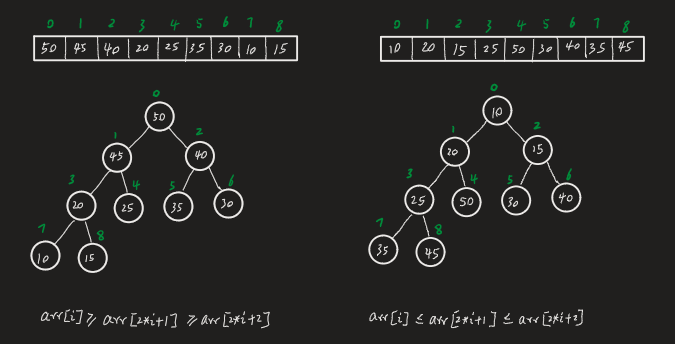
3. 堆类似完全二叉树，左右子节点大小顺序无规定
4. 大顶堆每个节点大于其左右子节点，
5. 小顶堆每个节点小于其左右子节点
6. 一般升序大顶堆，降序小顶堆

流程

1. 将数组以最大堆重新排序
2. 将最大值与最小值替换，并移除heap最大值(数组第一位与最后一位交换并缩小范围)
3. 重复1，2直到剩最后一个

public void sort(int arr[]){
    int n = arr.length;

    // Build heap (rearrange array)
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
    // One by one extract an element from heap
    for (int i = n - 1; i > 0; i--) {
        // Move current root to end
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;

        // call max heapify on the reduced heap
        heapify(arr, i, 0);
    }
}

// To heapify a subtree rooted with node i which is
// an index in arr[]. n is size of heap
void heapify(int arr[], int n, int i)
{
    int largest = i; // Initialize largest as root
    int l = 2 * i + 1; // left = 2*i + 1
    int r = 2 * i + 2; // right = 2*i + 2

    // If left child is larger than root
    if (l < n && arr[l] > arr[largest])
        largest = l;

    // If right child is larger than largest so far
    if (r < n && arr[r] > arr[largest])
        largest = r;

    // If largest is not root
    if (largest != i) {
        int swap = arr[i];
        arr[i] = arr[largest];
        arr[largest] = swap;

        // Recursively heapify the affected sub-tree
        heapify(arr, n, largest);
    }
}

假设数组为12 21 13 15 6 17
大顶堆数组移动
12 21 17 15 6 13
12 21 17 15 6 13
12 21 17 15 6 13
21 12 17 15 6 13
21 15 17 12 6 13

---

替换，重排序，并缩小范围
13 15 17 12 6 21
17 15 13 12 6 21
6 15 13 12 17 21
15 6 13 12 17 21
15 12 13 6 17 21
6 12 13 15 17 21
13 12 6 15 17 21
6 12 13 15 17 21
12 6 13 15 17 21
6 12 13 15 17 21